Siapa bilang Jim Carrey nggak tahu fisika? Coba lihat deh video yang diambil pada talk show "Late Night with Conan O'Brien".
Yang mereka bicarakan itu adalah paper beneran yang ditulis oleh Dr. Gabrielse yang berjudul "Stochastic Phase Switching of a Parametrically Driven Electron in a Penning Trap" yang dipublikasi di Physical Review Letter:
Wah…. jadi beneran tuh Jim Carrey ngerti fisika? Ck..ck..ck…
Transkrip pembicaraan:
(CO : Conan O’Brien, JC: Jim Carrey, MW: Max Weinberg)
CO : You're deeper than that. I know you're into a lot of reading. What are you reading these days? What are you studying? What do you into?
JC : I tell ya. I love, I absolutely love reading. I am a huge reader. And when I pick up something, I just can't put it down, you know. Like quantum physics. That's my favorite.
CO : Quantum physics? What are you talking about quantum physics? What?
JC : I was just reading this incredible paper on the stochastic phase-shifting of the parametrically-driven electron in a Penning trap; and apparently, a bistability arises dynamically in the specific parametrically-driven systems, because the phase 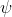 of the electron’s steady-state oscillation can either have the two values separated by
of the electron’s steady-state oscillation can either have the two values separated by 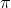 .
.
CO : Yea… that's crazy, you know. That's amazing. (Claps....) That's incredible. You know, it’s funny, what shocks me about an electron in a Penning trap is that most amplitude collapses are accompanied by a phase flip. Given that the rate of escape from the trap depends exponentially on an activation energy E as the diffusion constant D approaches 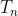 and approaches
and approaches 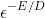 .
.
JC : Absolutely. Absolutely! No question there.
CO : We talked about that.
JC : Of course.
MW : I don’t know about that, Conan. Have you considered that the parametric driving force excites a nearly-resonant electron oscillation at the drive frequency, 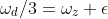 ? It’s a classic example of the period-doubling that occurs when a linear oscillator is strongly driven.
? It’s a classic example of the period-doubling that occurs when a linear oscillator is strongly driven.
MW : Yeah.
MW : You’re right.
good finding, thanks! aku ga pernah nonton conan, lbh suka jay leno, makanya ga pernah nemu ini, padahal aku fans jim carey.
ReplyDeleteIni juga saya tahunya waktu Dr. Gabrielse singgah ke kampus saya. Dia pakai video ini buat pengantar kolokium-nya dia :P Tapi lucu juga sih videonya, he..he...
ReplyDeleteMax Weinberg seharusnya lbh tau fisika, malu2in Steven Weinberg, aja :)
ReplyDelete